نموذج حل امتحان الجبر مرحلة اولى 2011

** الاجابة **


السؤال الأول ( إجباري ) :


اختبار الجبر ثانيه ثانوى 21-6-2011

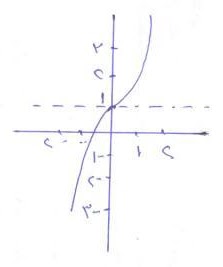
ا)
- نقطة التماثل س= 0 , ص= 1
- من الرسم نستنتج التالي :
مدى الدالة = ح
إطرادها = تزايدية على ح
النوع = ليست زوجية وليست فردية

ب)
المتتابعة هي (25,22,19,16,...........) -
- قيمة الحد الخامس عشر = 58


الاسئلة من الثاني إلى الخامس إختياري ويكفي الاجابة عن ثلاثة فقط منهم
السؤال الثاني :
أ)
- س = 1.5 تقريباً

ب)
- المتتابعة هي (6,12,24,48,...........)
- يتم اثبات انا |ر| < 1 حيث ان ر= 0.5
- مجموع عدد غير منته من حدود المتتابعة = 96



السؤال الثالث :
أ)
- المتتابعة هي ( 20,16,12,8,............)

ب)
{1.5} = م.ح
ويرفض الحلان 3 , -1



السؤال الرابع:
أ)
{0 , 4} = م.ح

ب)
- ك = 2
- المتتابعة = (16,8,4,2,.............)
- عدد الحدود التي يجب أخذها ليكون المجموع 510 = 8 حدود



السؤال الخامس :

اختبار الجبر ثانيه ثانوى 21-6-2011


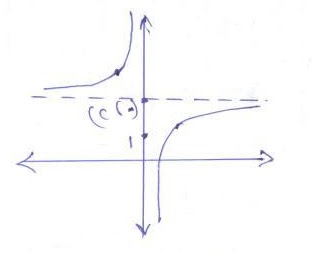
- محوري التماثل : س=0 , ص=2
- من الرسم ينتج الاتي :
{0} - ح =المجال

{2} - ح =المدى

ب)
- البرهان :
بفرض ان لوغاريتم أ للأساس ب = م -------> رقم 1
ب أس م = أ
ب = أ أس 1/م
لوغاريتم ب للأساس أ نعوض فيه عن قيمة ب
= لوغاريتم أ أس 1/م للأساس أ
=1/م(لوغاريتم أ للأساس أ)
لوغاريتم ب للأساس أ = 1/م -------> رقم 2
بضرب رقم 1 في رقم 2
ينتج المطلوب إثباته
- عند حل المعادلة نستخدم القانون السابق اثباته
حيث أن لوغاريتم س للأساس 2 = 1/(لوغاريتم 2 للأساس س)
وبعد حل المعادلة نستنتج ان :
{8 , 2} = م.ح
ويمكن التحقق من ذلك عن طريق التعويض في المعادلة بهذة القيم

بالتوفيق للجميع ........................